ブリッジ回路と言うと変わった形の配線構造の絵をよく見ますが、どんな意味があるのでしょうか。
今回はブリッジ回路の概要と、どんな用途に活用されているのかについて解説したいと思います。
こちらの記事は動画でも解説しているので、動画の方がいいという方はこちらもどうぞ。
ブリッジ回路とは
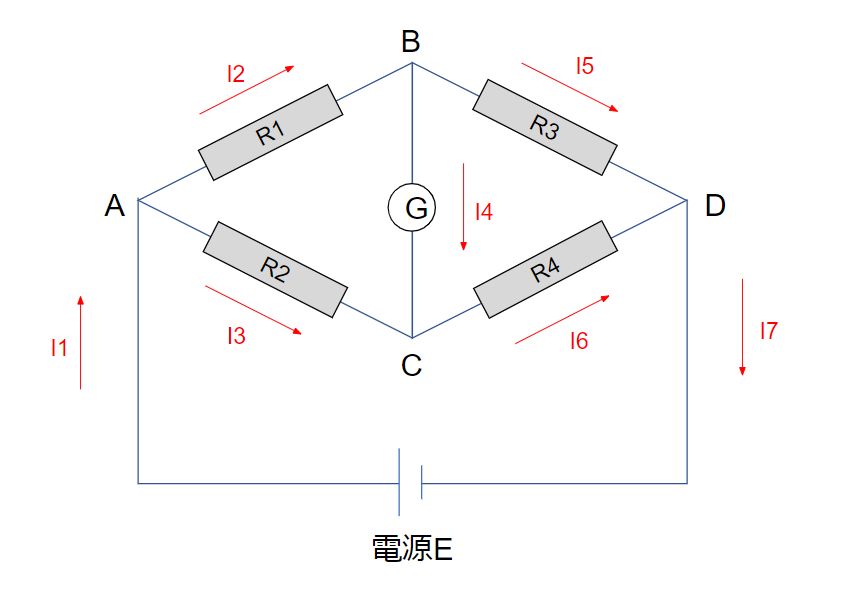
回路を構成する配線が2つの並列回路に分かれて、その2つの線間を別の配線でつないだ時、この橋渡しされた構造をブリッジ回路と呼びます。
イラストの中のGは検流計です。検流計は電流の大きさと、電流の向きを検出できることができます。
ここではこの構造を流れる電気が、どんな様子を見せるか説明します。電気を学んだ方はご存知の、キルヒホッフの法則という言葉が出てきます。
一つ目に説明する現象は電流の入力と出力は同じというものです。上記のイラストで言うと、
$$I1 = I2 + I3$$
$$I5 + I6 = I7$$
$$I1 = I7$$
が成り立ちます。当たり前のように見えますが、大事な前提条件です。これをキルヒホッフの第1法則と呼びます。
次に電圧の様子を見たとき、閉回路における起電力と電圧降下は等しくなると言う現象が起こります。イラストで言うと、
$$E = R1×I2 + R3×I5$$
$$E = R2×I3 + R4×I6$$
$$R1×I2 + G×I4 = R2×I3$$
$$R3×I5 = G×I4 + R4×I6$$
という関係があります。ここでのEは電源電圧、Gは検流計の内部抵抗を表しています。この関係を、キルヒホッフの第2法則と呼びます。
ブリッジ回路を用いる理由
上記のブリッジ回路で、R3は自在に抵抗値が変えられるとします。各抵抗R1〜 R4の値の関係で、R3が特定の値を取った時にブリッジ構造部B-Cに電位差がなくなる時があります。このとき、I4 = 0となります。
B-C間に電位差がないので、
$$R1×I2 = R2×I3$$
$$R3×I5 = R4×I6$$
という並列回路の電圧が等しいという関係になります。両式と、I2 = I5、I3 = I6という関係式を当てはめると、
$$\frac{R1}{R2} = \frac{R3}{R4}$$
という関係式となります。(この状態を満たす電気回路のことを、ホイートストンブリッジと呼びます。)
ここで、自在に可変できる抵抗器R3に加え、R4が未知の値の抵抗器だった場合どうなるでしょうか?
可変抵抗器の値を変更しながら、検流計Gが0を示すように調整し、上式に当てはめることでR4を求めることができますよね。
センサーとして物理的に検出しづらい場合でも、ブリッジ回路で抵抗値を計測することで、より精度の高い値を読み取ることができます。
実際にはこの抵抗変化を、定電流もしくは定電圧をかけた時の電圧値や電流値として計測しているようです。
また、検出部を増やしたり、測定方法を工夫したりすることで、外部環境(周囲温度や配線の長さ)に影響されない測定を行うことが可能です。
ブリッジ回路の使用例
ブリッジ回路は以下のような機器に活用されています。
重量計(はかり)
ロードセルは力(トルク)を計測するセンサーの一つで、代表的なものとして重量を測定する、いわゆる“はかり”があります。力に比例して検知部にひずみが生じます。
この検知部をひずみゲージと呼びます。ゲージにかかる力によって発生する金属の伸縮を感知して、重さに換算しています。
圧力センサー
ひずみゲージ式と呼ばれるタイプは、ダイヤフラム(金属の薄い膜)のひずみの大きさによって圧力を感知します。物理的な変化はわずかに見えますが、この変化をひずみゲージ抵抗を用いて感知します。
-

【圧力センサー】圧力センサーの測定原理とは?
続きを見る
加速度センサー
センサーに加速度が加わると、内部の金属体(重錘)に力が加わり、その変化をひずみゲージで検出するというタイプがあります。車両の加速度計測などに用いられています。
振動センサー
解説は上記の加速度と計測と被るのですが、加速度計測により振動値を計測するタイプがあります。こちらも同様に、加速度変化を歪みで計測し、振動値に換算します。回転機の振動計測などに用いられています。
まとめ
・ブリッジ回路は橋渡し構造をした回路で、実用的に用いられている
・各種センサーの測定原理としてブリッジ回路を用いたひずみゲージ計測が活用されている
センサーの世界は奥が深いですね。
原理を理解していくことで、測定精度や測定限界を知ることになり、皆様の現場でのより正確なデータ計測(もしくは適度な精度にスペックダウンすることでのコストカット)にも活かせるかと思います。