オットーサイクルは、ガソリンエンジンやガスエンジンなどで利用される火花点火の熱サイクルで、ガソリンなどの燃料が持つ熱エネルギーをピストン運動に変換します。
この記事ではオットーサイクルとは何か、基本的な考え方や効率の計算方法について解説します。
オットーサイクルとは?

オットーサイクルは、内燃機関の一種で、ガソリンエンジンの基本的な動作原理を説明する理論的なサイクルです。
1876年にドイツの技術者ニコラウス・オットーによって発明されました。オットーサイクルは、吸気、圧縮、燃焼(爆発)、排気の4つの工程から成り立っています。
このサイクルの特徴は、一定の圧縮比と熱効率を持ち、燃焼過程でのエネルギーを効率的に機械的な仕事に変換することです。特に、自動車のガソリンエンジンに広く採用されており、その効率とパフォーマンスが高く評価されています。
-

【熱機関】外燃機関と内燃機関の違いとは?
続きを見る
オットーサイクルの基本サイクル
オットーサイクルの基本は次の4つの工程で表すことができます。
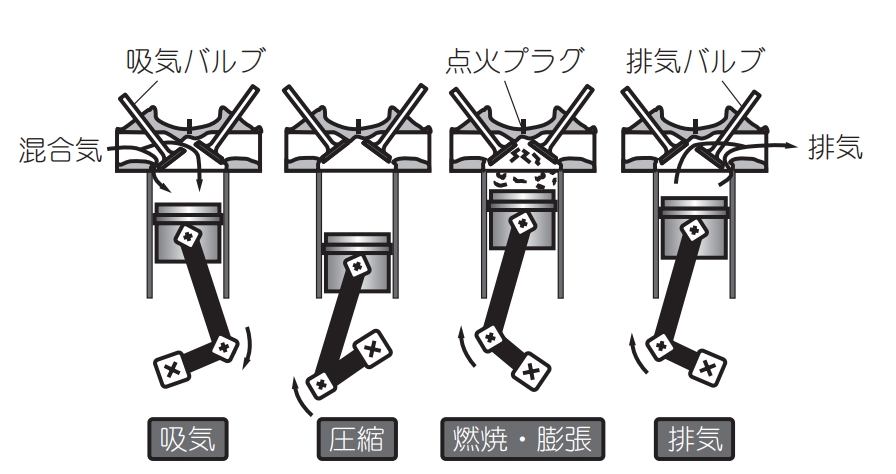
(出展:熱力学の基本のきPDF)
吸気行程
吸気行程では、ピストンがシリンダー内を下がり、吸気バルブが開くことで外部から空気と燃料の混合気がシリンダー内に吸い込まれます。この段階での混合気の取り込みは、後続の圧縮行程と燃焼行程におけるエネルギー生成の基礎となります。
吸気行程の効率は、エンジンの全体的な性能や燃費に直接影響するため、エアフィルターや吸気経路の設計が重要です。
圧縮行程
圧縮行程は、吸気行程で取り込まれた混合気を圧縮する段階です。ピストンがシリンダー内を上昇することで、混合気の体積が減少し、その結果、圧力と温度が上昇します。この圧縮された状態は、次の燃焼行程での効率的な燃焼を可能にします。
高い圧縮比を実現することで、エンジンの熱効率を向上させることができますが、ノッキング(異常燃焼)のリスクもあるため、バランスが重要です。
燃焼行程(爆発行程)
燃焼行程は、圧縮された混合気がスパークプラグによって点火され、急激に燃焼する行程です。
この燃焼により発生した高圧ガスがピストンを強制的に下方に押し出し、これがエンジンの回転力となります。燃焼行程の効率は、燃焼の均一性と速度に依存します。最適な点火タイミングと燃料の質が、この行程でのエネルギー変換効率に大きく影響します。
排気行程
排気行程は、燃焼後のガスをシリンダー外に排出する行程です。ピストンが再び上昇し、排気バルブが開くことで、燃焼ガスがシリンダーから外部へ排出されます。この工程は、次のサイクルで新しい混合気を取り込むための準備となります。
排気行程の効率を高めるためには、排気経路の設計や排気バルブのタイミングが重要です。また、排出されるガスの処理も環境保護の観点から重要な要素です。
一連のサイクルを理解するのにわかりやすい動画を作成したので載せておきます。
ピストンの動きを回転運動にするためにはクランクシャフトという機器によって行われます。
オットーサイクルの線図
オットーサイクルの挙動を視覚的に理解するためには、P-v線図(圧力-体積線図)とT-s線図(温度-エントロピー線図)の二つの線図が有効です。
これらの線図により、サイクルの各工程における状態変化を視覚的に理解できます。
P-v線図
P-v線図は、圧力(P)と体積(v)の関係を示すグラフで、オットーサイクルの各工程を視覚的に表現します。
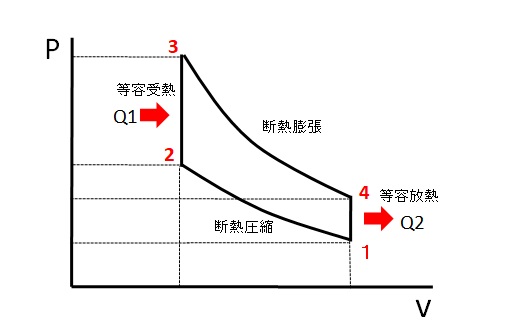
- 1⇒2 吸気行程
吸気バルブが開き、ピストンが下降することでシリンダー内の体積が増加し、圧力がほぼ一定のまま低下。 - 2⇒3 圧縮行程
吸気バルブが閉じ、ピストンが上昇することでシリンダー内の体積が減少し、圧力が上昇。 - 3⇒4 燃焼行程(爆発行程)
圧縮された混合気が点火され、体積はほぼ一定のまま急激に圧力が上昇。 - 4⇒1 排気行程:
排気バルブが開き、ピストンが再び上昇することでシリンダー内の体積が減少し、圧力が低下。
P-v線図の場合は、1で吸気して1⇒2で圧縮されることで圧力が上昇します。2⇒3で火花によって爆発し、3⇒4で膨張することで圧力が下がります。そして最後に4⇒1で排気されて圧力が下がります。
この時、2⇒3で発生したQ1の熱量から排気で捨てられたQ2を引いたものが動力に変換されたと考えます。
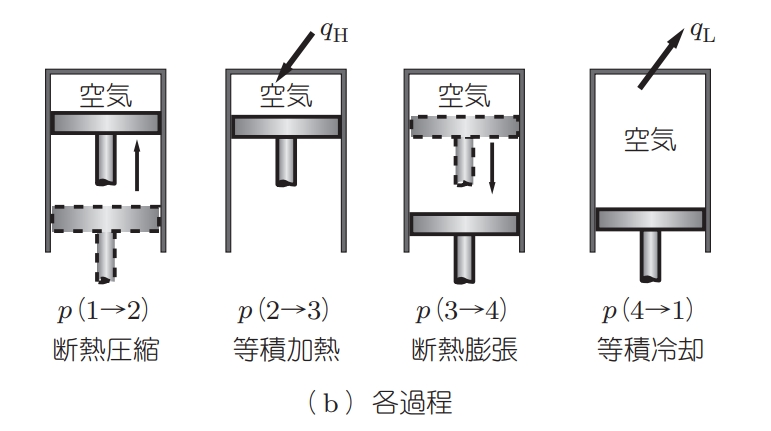
(出展:熱力学の基本のきPDF)
T-s線図
T-s線図は、温度(T)とエントロピー(s)の関係を示すグラフで、オットーサイクルの熱力学的挙動を理解するために重要です。
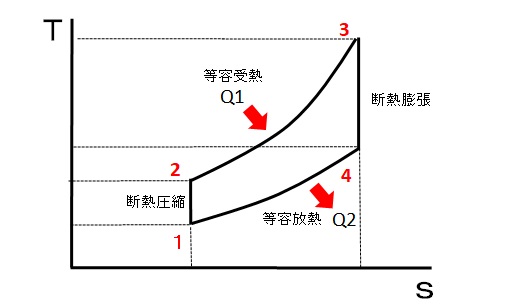
- 1⇒2 吸気行程
吸気バルブが開き、混合気がシリンダー内に吸い込まれる際、エントロピーが増加し、温度はほぼ一定に保たれる。 - 2⇒3 圧縮行程
吸気バルブが閉じ、混合気が圧縮されることでエントロピーがほぼ一定のまま温度が上昇。この過程は断熱圧縮として扱われる。 - 3⇒4 燃焼行程(爆発行程)
圧縮された混合気が燃焼し、エントロピーが急増し、温度も急上昇。この過程は等容燃焼として扱われる。 - 4⇒1 排気行程
排気バルブが開き、燃焼ガスが排出される際、エントロピーが減少し、温度も低下。
T-s線図では、断熱膨張と断熱圧縮の際に外部との熱のやり取りがないのでエントロピーが変化しないというところがポイントです。圧縮されると分子の動きが早くなるので、それがすべて熱エネルギーに変換されるというイメージです。
圧縮と膨張の2種類の等エントロピー変化があることを覚えておきましょう。
-

【熱力学】エンタルピーって何?内部エネルギー、エントロピーとの違いは?
続きを見る
オットーサイクルの熱効率
次にオットーサイクルの熱効率の考え方を見てみましょう。
オットーサイクルの目的は、燃料などの熱エネルギーを動力エネルギーに変換することなので、熱効率を表す場合は「どれだけの熱を取り込み、どれだけの熱を捨てたか」が重要になります。
つまり、何%の熱エネルギーを動力エネルギーとして取り出すことができたかどうかは次の式で表すことができます。
$$η=1-\frac{Q_2}{Q_1}$$
η:効率 Q1:入熱 Q2:出熱
この式をもとに、効率を高めるためにはどうすればいいかを考えていきます。
まずは作動流体をm[kg]の理想気体とします。この時、入熱、出熱共に体積一定の定容状態での変化となるため、Q1、Q2はそれぞれ次の式で表すことが出来ます。
$$Q_1=mc_v(T_3-T_2)$$
$$Q_2=mc_v(T_4-T_1)$$
cv:定容比熱 T1~T4:それぞれの温度[K]
定容比熱は体積一定の場合の気体の比熱を表しています。定圧比熱cpと定容比熱cvの関係は次の記事を参考にしてください。
-

【熱力学】定圧比熱と定積比熱、気体の比熱が2種類あるのはなぜ?
この式を最初の式に当てはめると次のように変換することができます。
$$η=1-\frac{T_4-T_1}{T_3-T_2}$$
1⇒2は断熱変化なのでT2はT1を用いて次のように表すことができます。これは断熱変化における変換公式の一つです。
$$T_2=T_1(\frac{V_1}{V_2})^{κ-1}$$
V1/V2を圧縮比εで表したとすると
$$T_2=T_1ε^{κ-1}$$
κ:比熱比(cp/cv) V1、V2:体積
一方、2⇒3は等容変化なのでT3は次の式で表すことができます。こちらも等容変化における変換公式の一つです。
$$T_3=T_2\frac{P_3}{P_2}$$
T2に先程の式を当てはめて、P3/P2を圧力上昇比ξで表したとすると
$$T_3=T_1ε^{κ-1}ξ$$
P2、P3:それぞれの圧力
同様に、3⇒4は断熱変化なのでT4をT3で表すと
$$T_4=T_3(\frac{V_3}{V_4})^{κ-1}$$
V1~V4の関係は次の式で表すことができます。
$$\frac{V3}{V4}=\frac{V2}{V1}=\frac{1}{ε}$$
これを上の式に代入すると
$$T_4=T_1ε^{κ-1}ξ(\frac{1}{ε})^{κ-1}=T1ξ$$
これらをすべて代入すると最終的に次のような式に変換することができます。
$$η=1-\frac{T_4-T_1}{T_3-T_2}$$
$$=1-( \frac{1}{ε} )^{κ-1}$$
細かい式の導出は覚える必要はありませんが、この式より、オットーサイクルの効率は圧縮比と気体の比熱比によって決まるということが分かります。
圧縮比、比熱比ともに高ければ高いほど効率は良くなります。但し、圧縮比が大きすぎると異常燃焼が発生するため、一般的には5~10が良いとされています。
圧縮比を上げるためには一般的に次のような方法がとられます。
- 燃料のオクタン価を上げる。
- 混合気を冷やす。
- シリンダ温度を下げる。
この辺りは車に詳しい方ならご存じかと思います。
-

【燃料】オクタン価とセタン価の違いは?
続きを見る
オットーサイクルの平均有効圧力
レシプロエンジンの能力を表す一つ指標として「平均有効圧力」があります。
平均有効圧力は、1サイクル中で変化するシリンダー内の圧力を一定だと仮定した値を表すことで、排気量に関係なくエンジンの評価をすることが出来ます。
熱交換器でいう対数平均温度差LMTDと似たような考え方です。
-

【熱交換器】対数平均温度差LMTDの使い方と計算方法
続きを見る
オットーサイクルの平均有効圧力は次の式で表すことが出来ます。
$$P_m=\frac{W}{V_s}$$
Pm:平均有効圧力、W:仕事、Vs:工程体積
有効平均圧力は仕事を工程体積で割ったものになります。これに先ほどの効率を計算する際に出てきた値を導入して変形すると最終的に次のようになります。
$$P_m=\frac{Q_1-Q_2}{V_1-V_2}$$
$$=\frac{mc_v[(T_3-T_2)-(T_4-T_1)]}{V_1-V_2}$$
$$=P_1\frac{(ξ-1)(ε^κ-ε)}{(κ-1)(ε-1)}$$
この式により、平均有効圧力は吸込圧力P1に比例することが分かります。また、圧縮比、比熱比、圧力上昇比も大きい方が仕事も大きくなるということが分かります。
オットーサイクルの計算問題
実際に数値を当てはめながら次の問題を解いてみます。
工程体積(排気量)2Lで圧縮比9.0のエンジンを積む自動車が得られる仕事W及び理論熱効率ηを求めよ。
このエンジンの圧縮はじめ圧力は0.1MPa、温度は70℃で最高温度は2000℃で作動流体は空気とする。但し、ガス定数を287[J/kgK]、定圧比熱を1.17[kJ/kgK]とする。
まず、仕事Wと理論熱効率を求める式を考えます。
$$W=Q_1-Q_2$$
$$=mc_v[(T_3-T_2)-(T_4-T_1)]・・・(1)$$
$$η=1-(\frac{1}{ε})^{κ-1}・・・(2)$$
問題文よりわかる値を整理します。
工程体積2Lより
$$V_1-V_2=2.0×10^{-3}・・・(3)$$
圧縮比9.0より
$$ε=\frac{V_1}{V_2}=9.0・・・(4)$$
その他の値は次のようになる。
$$P_1=0.1×10^6$$
$$T_1=70+273$$
$$T_3=2000+273$$
これらの値を利用して(1)と(2)を解いていきます。
まず、シリンダの体積を求めます。
(3)と(4)の連立方程式を解くと
$$V_2=\frac{V_1-V_2}{ε-1}$$
$$=\frac{2.0×10^{-3}}{9.0-1}=2.5×10^{-4}$$
$$V_1=εV_2=2.25×10^{-3}$$
次に空気の質量を求めます。
状態方程式より
$$P_1V_1=mRT_1$$
$$m=\frac{P_1V_1}{RT_1}$$
$$=\frac{0.1×10^6×2.25×10^{-3}}{287×(70+273)}$$
$$=2.29×10^{-3}$$
次に比熱比κを求めます。
$$c_v=c_p-R$$
$$=1.17×10^3-287=883$$
$$κ=\frac{c_p}{c_v}=\frac{1170}{883}=1.325$$
最後に各状態での温度を求めます。
$$T_2=T_1ε^{κ-1}=343×9^0.325=701[K]$$
$$T_4=\frac{T_3}{ε^{κ-1}}=\frac{2273}{9^0.325}=1113[K]$$
これらを(1)(2)に当てはめると、欲しい答えが導出できます。
$$W=1622[J]=1.622[kJ]$$
$$η=0.510$$
まとめ
- オットーサイクルはエンジンの理想的な熱サイクル。
- 2つの断熱変化と2つの等容変化から成り立つ。
- 圧縮比を上げると理論熱効率が上がる。
- 平均有効圧力は吸込圧力に比例する。
資格試験の場合、オットーサイクルはランキンサイクルほどの出題頻度はありませんが、P-v線図やT-s線図を聞いてくる問題は良く出題されるので全体をよく理解しておきましょう。
-

【熱機関】熱機関とは何か、概要や種類について解説します
続きを見る