カルノーサイクルは温度の異なる２つの熱源で動作する熱サイクルの１種です。熱機関について学ぶ時に最初に出てくる熱サイクルで、理論上の最大効率を示します。
今回は、カルノーサイクルとは何か？について詳しく解説してみたいと思います。
カルノーサイクルとは？
カルノーサイクルは、1824年にフランスの物理学者ニコラ・レオナール・サディカルノーが考案した理想的な熱サイクルです。18世紀半ばから19世紀にかけて起こった産業革命で、いかに効率よく燃料から動力を生み出すかという課題が出てきたことから考案された理論サイクルです。
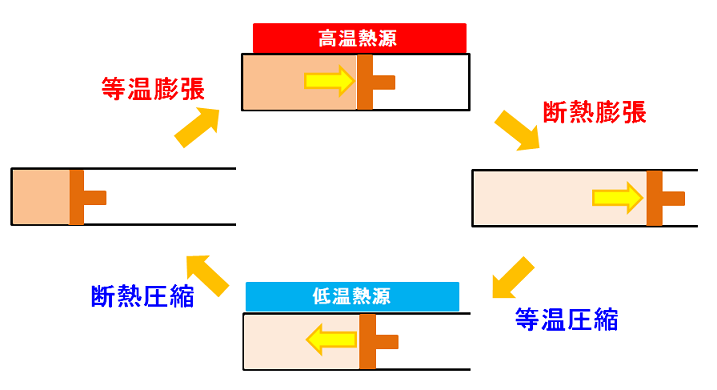
高温熱源と低温熱源を利用して、等温膨張、断熱膨張、等温圧縮、断熱圧縮の４つの過程を繰り返し、熱エネルギーを動力に変換します。等温変化は外部との熱のやり取りがある状態、断熱変化は外部との熱のやり取りがない状態での膨張、圧縮を表します。
カルノーサイクルは理想的なエンジンの動きを表し、その効率は理論上の最大値を示します。ここでいう効率とは、燃料の熱がどれほど動力としての仕事に変化したかを表します。
カルノーサイクルでは高温熱源の温度と低温熱源の温度だけで効率が計算できるというのも大きな特徴です。
-
【タービン】タービン効率の考え方、熱落差ってなに？
続きを見る
-
【ボイラー】ボイラー効率って何？100%を超えるのはなぜ？
続きを見る
カルノーサイクルの工程
カルノーサイクルは次の4つの工程で完結します。
- 等温膨張（温度一定で熱源から熱をもらい膨張）
- 断熱膨張（熱のやり取りをなくし膨張させる）
- 等温圧縮（温度一定で放熱させて圧縮する）
- 断熱圧縮（熱のやり取りをなくし圧縮する）
このサイクルを図に表すと次のようになります。
それぞれの工程について見てみます。
初期状態⇒等温膨張
初期状態はピストンの中に空気が入っていると考えてください。ここに高温の熱源を近づけると熱が伝わり、ピストンの中の空気が膨張します。この時、温度は一定で熱源からもらうエネルギーはすべて膨張する（外部に仕事をする）ために利用されます。これを等温変化といいます。
-
【熱力学】定圧比熱と定積比熱、気体の比熱が2種類あるのはなぜ？
続きを見る
熱が伝わることで空気が膨張する仕組みは、熱力学第１法則を考えるとよくわかります。
熱力学第１法則
$$ΔQ=ΔU+ΔW$$
$$ΔW=Δ(PV)$$
Q：熱エネルギー、U：内部エネルギー、W：仕事
熱力学第１法則から温度Ｔ一定のまま変化したとすると、温度に関する内部エネルギーは変化しないのでもらった熱は仕事に変換されるということが分かります。
等温変化の圧力、体積、温度の関係は次の式でも表すことができます。
等温変化の圧力、体積、温度の関係
$$Q=mRTln\frac{V2}{V1}=mRTln\frac{P2}{P1}$$
m：質量、R：ガス定数、T：温度
-
【熱力学】エンタルピーって何？内部エネルギー、エントロピーとの違いは？
続きを見る
等温膨張⇒断熱膨張
次に、外部との熱のやり取りがない状態で内部の空気が膨張していきます。熱のやり取りがない状態で気体が膨張すると、熱力学第１法則から内部の温度は低下します。
外部と熱のやり取りがない状態変化を断熱変化と呼びます。断熱変化の温度と体積の関係は次の式で表せます。
断熱変化の圧力、温度、体積の関係
$$PV^κ=一定$$
$$TV^{κ-1}=一定$$
$$κ=\frac{cp}{cv}$$
κ：比熱比、cp：定圧比熱、cv：定積比熱
この式を見ると、等温変化では体積が増加すると温度が低下することが分かります。
-
【熱力学】定圧比熱と定積比熱、気体の比熱が2種類あるのはなぜ？
続きを見る
断熱膨張⇒等温圧縮
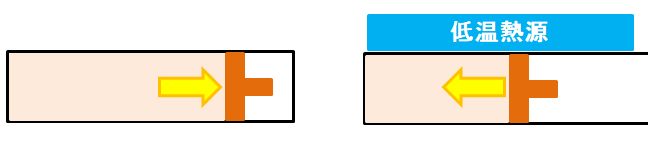次に、低温熱源を利用して等温変化でピストン内の空気から熱を奪います。等温膨張とは逆の動きで内部の気体が収縮していきます。
これを等温圧縮といいます。この時、内部の圧力は下がり、体積は小さくなります。
断熱圧縮⇒初期状態
次に熱のやり取りがない状態で、気体が圧縮され初期の状態に戻ります。これを断熱圧縮といいます。そして、また高温熱源から熱をもらい等温膨張が始まります。
このように、カルノーサイクルは高温熱源と低温熱源を利用して一連のサイクルを完結させます。
一連の流れをアニメーションで作成したのでこちらも載せておきます。
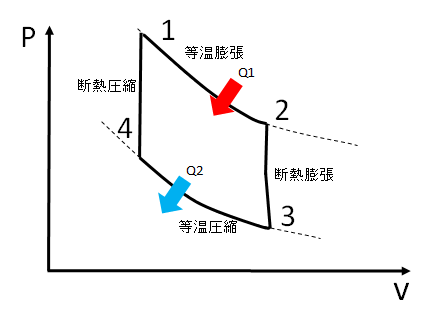
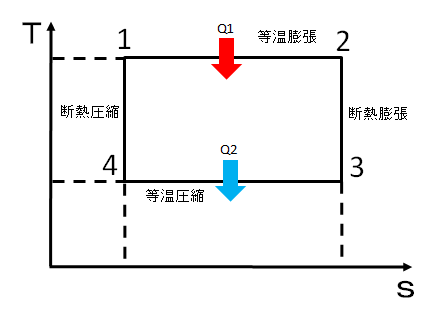
カルノーサイクルのPV線図とT-s線図
熱機関には、圧力Pと体積Vの関係を表したPV線図と温度TとエントロピーSの関係を表したT-s線図というものがあります。
カルノーサイクルのPV線図とT-s線図は次のようになります。
カルノーサイクルPV線図
カルノーサイクルTs線図
それぞれの状態に１～４の番号を付けています。赤い矢印が受熱、青い矢印が放熱を表しています。
- １⇒２ 等温膨張
- ２⇒３ 断熱膨張
- ３⇒４ 等温圧縮
- ４⇒１ 断熱圧縮
これらの動作は種類に関係なく、気体、高温熱源、低温熱源の３つがそろえば実現することができます。断熱変化は外部との熱のやり取りがなく、等エントロピー変化となっています。
実際の熱機関では、ピストンとシリンダーとの摩擦などによりエントロピーは増加するので等エントロピー変化はあくまで理想的な状態を表しています。
カルノーサイクルの熱効率は？
熱機関の目的は、熱源から動力を取り出すことです。与えた熱エネルギーがどの程度、動力に変わったかを表すものが熱効率です。そして、カルノーサイクルが考案された理由はどの条件を変化させれば熱効率を上げることができるか？ということでした。
カルノーサイクルでは高温熱源と低温熱源の温度差によって熱機関の効率が決まることが分かります。
カルノーサイクルの熱効率は次の式で表すことができます。
$$η=\frac{T1-T2}{T1}$$
※Tの単位はK（ケルビン）です。
実際に熱機関の効率を求めてみましょう。
熱機関の効率は、分母に与えた「熱源のエネルギー」分子に「取り出せる仕事」を置き次のように表すことができます。
$$η=\frac{W}{Q1}$$
η（イータ）：熱効率、W：取り出せる仕事（Ｊ）、Q1：熱源のエネルギー（Ｊ）
ここで、熱機関自体に摩擦などのエネルギー損失が全くないと仮定して、失った熱エネルギーはすべて仕事に変換されると仮定すると「取り出せる仕事W」は次の式で表すことができます。
$$W=Q1-Q2$$
Q1：熱源のエネルギー（Ｊ）、Q2：失った熱量（Ｊ）
これを代入すると
$$η=\frac{Q1-Q2}{Q1}$$
ここから、等温変化と断熱変化の式からカルノーサイクルの効率を温度Tだけで表せるように持っていきます。
カルノーサイクルで等温変化するタイミングは１⇒２と３⇒４の２つです。
- 高温熱源（T1）から熱をもらう
- 低温熱源（T2）へ熱を与える
高温熱源の温度をT1、低温熱源の温度をT2とすると、等温変化の時の熱量変化は次の式で表すことができます。
$$Q1=mRT1ln\frac{P1}{P2}・・・①$$
$$Q2=mRT2ln\frac{P4}{P3}・・・②$$
m：質量、R：ガス定数、P：圧力
一方、断熱変化の時には、次のポアソンの式が成り立ちます。
$$PV^κ=一定$$
このポアソンの式を２⇒３と４⇒１に当てはめると、次の式が成り立つことが分かります。
$$\frac{P1}{P2}=\frac{P4}{P3}・・・③$$
①②③の式から
$$\frac{Q1}{Q2}=\frac{T1}{T2}$$
という式が成り立ち、これを効率の式に当てはめるとカルノーサイクルの熱効率は最終的に次の式で表すことができます。
$$η=\frac{T1-T2}{T1}$$
※Tの単位はK（ケルビン）です。
つまり、熱機関の最大効率は高温熱源の温度を上げるか、低温熱源の温度を下げてやれば上がります。
熱機関で発生する正味の効率は？
カルノーサイクルから、高温熱源と低温熱源の温度によって取り出せる最大仕事は変化するということが分かりました。
しかし、実際には上の式で出した効率を出すことはできません。それは、熱が仕事に変化する過程で気体と機械との摩擦（内部損失）や機器自体の摩擦（外部損失）が発生するからです。
実際にはこれらを加味したうえで効率は計算されます。
$$η=η1η2η3$$
理論熱効率：η1、機関効率：η2、機械効率：η3
タービン効率についてはこちらの記事でも書いてますので参考にしていただければと思います。
-
【タービン】タービン効率の考え方、熱落差ってなに？
続きを見る
カルノーサイクルの問題を解いてみよう
カルノーサイクルの式を利用して、実際に最大効率を計算してみましょう。
問題
ある蒸気をつかって発電を行う蒸気タービンについて考えます。
入口蒸気温度250℃、出口の復水の温度が40℃の場合、このタービンの理論最大効率はいくらでしょう？
これに対する解答は次のようになります。
カルノーサイクルの効率の式を使って
$$η=\frac{T1-T2}{T1}$$
ここで
$$T1=273+250$$
$$T2=273+40$$
より
$$η≒0.40$$
最大効率は40%だとわかります。
-
【熱機関】ランキンサイクルとは？わかりやすく徹底解説します
続きを見る
まとめ
- カルノーサイクルは理想的な熱サイクル
- ２つの等温変化と２つの断熱変化で構成される
- 最大効率は入出の温度のみで決まる
- 実際には内部損失や外部損失を考慮した効率になる
熱機関を理解するのに、カルノーサイクルの考え方は必須なのでしっかりと押さえておきましょう。
実際に計算するときは、温度が℃ではなく絶対温度Ｋ（ケルビン）で計算しないといけないことに注意しましょう。
-
【熱機関】熱機関とは何か、概要や種類について解説します
続きを見る
