プラントや工場では、発生する熱エネルギーを無駄にしないために様々な工夫がされています。
その1つに熱交換器を設置して熱回収をするなどがありますが、熱交換器などの計算を行う際には対数平均温度差が必要です。今回は、対数平均温度差とは何かについて解説してみたいと思います。
こちらの記事は動画でも解説しているので、動画の方がいいという方はこちらもどうぞ。
対数平均温度差LMTDとは?
対数平均温度差(LMTD)とは、全体の伝熱量が等しくなるような計算上の温度差のことです。LMTDはLogarithmic Mean Temperature Differenceの略になります。
熱交換器では高温のものと低温のものを触れさせることによって熱交換を行います。しかし、当然のことながら熱交換器内でも場所によって温度差が違います。
そこで、どこをとっても同じ温度差になるように計算で近似値を求められるようにしたものが対数平均温度差の考え方です。対数平均温度差を利用することで、ある流体が熱交換器で熱交換できる熱量を計算することができます。
対数平均温度差は次の式で表すことができます。ΔTa、ΔTbについては後程解説します。
対数平均温度差は熱交換器の伝熱面積を計算するときや、各条件の時の伝熱量を計算する際に使用します。
-

【熱交換器】熱交換器の伝熱面積計算方法
続きを見る
対数平均温度差LMTDの計算
対数平均温度差を計算する際には、入口と出口の温度差が必要になります。
熱交換を行う際には、それぞれの流体の流れ方向で並流と向流の2つに分けることができます。
流体が並行して流れるものが並流、向かい合って流れるものが向流と呼ばれます。対数平均温度差は向流のほうが大きくなり、熱交換量も大きくなります。
対数平均温度差を計算する時には、入口の温度差ΔTaと出口の温度差ΔTbが必要になります。式で表すと次のようになります。
$$T_b=T[④]-T[②]$$
$$ΔT[LMTD]=\frac{ΔT_a-ΔT_b}{ln(ΔT_a/ΔT_b)}$$
対数平均温度差LMTDの使い方
対数平均温度差は次のように利用することができます。
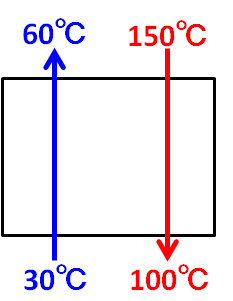
高温流体150℃⇒100℃、低温流体30℃⇒60℃、向流、伝熱面積A=1.5m2、熱通過率K=1000kJ/m2h℃の時の1時間当たりの伝熱量を求める。
この場合、まず対数平均温度差を求めます。
$$Tb=100℃-30℃$$
$$ΔT[LMTD]=\frac{90-70}{ln(90/70)}$$
$$ΔT[LMTD]=79.6℃$$
伝熱量はQ=AKΔT[LMTD]で計算することができるので、これらをかけ合わせれば
このように計算することが可能です。
まとめ
- 対数平均温度差は温度差の近似値。
- 入出の温度差が分かれば計算できる。
- 熱交換器の伝熱量を計算する際に使用する。
熱交換器の計算をするときは、対数平均温度差の考え方は必須なのでぜひ覚えておきましょう。